Light – Reflection and Refraction

Reflection of Light

What is Light?

• We see objects because they reflect light.
• In the dark, we can’t see anything until light is present.
• Sunlight helps us see during the day by reflecting off objects into our eyes.
• Transparent mediums let light pass through them, making objects visible.

Properties of Light

• Straight Line Travel: Light usually travels in straight lines.
• Ray of Light: A narrow beam of light is called a ray.
• Diffraction: When light bends around small objects, it is called diffraction (studied in higher classes).
• Wave and Particle Nature: Light behaves both as waves and particles (advanced concept).

• Optical Phenomena: Light’s properties help us understand:
  • Image formation by mirrors
  • Twinkling of stars
  • Rainbow colors
  • Bending of light in different media

Reflection of Light

• Reflection: When light bounces off a surface.
• Laws of Reflection:
  1. Angle of incidence = Angle of reflection.
  2. Incident ray, reflected ray, and normal (perpendicular to the surface) all lie in the same plane.
• Plane Mirrors: Form virtual, erect images, same size as the object, and laterally inverted.

Image Formation by Plane Mirrors

• The image is virtual (cannot be projected on a screen), erect (upright), and laterally inverted (left-right reversed).
• The size of the image is equal to the object, and it’s as far behind the mirror as the object is in front.

Spherical Mirrors

• Concave Mirrors: Reflecting surface curves inwards, like the inside of a spoon.
  • Used in torches, headlights, shaving mirrors, and solar furnaces.
  • Forms real or virtual images depending on the object position.
• Convex Mirrors: Reflecting surface curves outwards, like the back of a spoon.
  • Used in vehicle rearview mirrors.
  • Always forms virtual, diminished, and erect images.

Spherical Mirrors: Key Terms

• Pole (P): The center of the mirror’s surface.
• Centre of Curvature (C): The center of the sphere from which the mirror is a part.
• Radius of Curvature (R): The distance from the pole to the center of curvature.
• Principal Axis: A straight line passing through the pole and the center of curvature.
• Principal Focus (F):
  • Concave Mirror: Parallel rays converge at this point after reflection.
  • Convex Mirror: Parallel rays appear to diverge from this point
• Focal Length (f): Distance between the pole and the principal focus.
• Aperture: The diameter of the reflecting surface of a spherical mirror.
  • In discussions, consider only mirrors with apertures much smaller than the radius of curvature.

Relationship Between Radius of Curvature and Focal Length

• Formula:

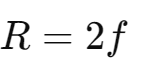
• Explanation: For spherical mirrors with small apertures, the radius of curvature is twice the focal length. The principal focus lies midway between the pole and the center of curvature.

Ray Diagrams for Spherical Mirrors

Introduction

• We can draw ray diagrams to study how spherical mirrors form images.
• Imagine an object in front of a mirror. Every small part of the object sends out rays.
• For simplicity, we use only two rays to find the image.

Key Rays for Ray Diagrams

1. Parallel Ray:
   • A ray parallel to the principal axis reflects through the principal focus (F) for a concave mirror.
   • For a convex mirror, it appears to come from the principal focus.
2. Focal Ray:
   • A ray passing through (or heading towards) the principal focus reflects parallel to the principal axis.
3. Center of Curvature Ray:
   • A ray passing through the center of curvature (C) reflects back on itself because it hits the mirror perpendicularly.
4. Oblique Ray:
   • A ray hitting the mirror obliquely at the pole reflects at an equal angle on the other side of the principal axis.

• Concave Mirror:
  • Rays parallel to the principal axis pass through the focal point after reflection.
  • Rays passing through the focal point reflect parallel to the principal axis.
  • Rays through the center of curvature reflect back on the same path.
• Convex Mirror:
  • Rays parallel to the principal axis appear to diverge from the focal point after reflection.
  • Rays directed towards the focal point reflect parallel to the principal axis.
  • Rays directed towards the center of curvature appear to come back along the same path.

Image Formation by Spherical Mirrors

A. Image Formation by Concave Mirrors

Summary

• The nature, position, and size of the image depend on the object’s position relative to P, F, and C.
• Images can be real or virtual, magnified, reduced, or the same size.

B. Image Formation by Convex Mirrors

Two Positions for Convex Mirrors

1. Object at Infinity:
   • Rays appear to come from a point (focus) behind the mirror.
2. Object at Finite Distance:
   • The image is diminished, virtual, and appears behind the mirror.

Sign Convention for Reflection by Spherical Mirrors

Introduction to Sign Conventions

• We use the New Cartesian Sign Convention for spherical mirrors.
• The pole (P) of the mirror is the origin.
• The principal axis of the mirror is the x-axis.

Conventions

1. Object Placement:
   • Always placed to the left of the mirror.
2. Distance Measurement:
   • All distances are measured from the pole (P).
3. Positive and Negative Distances:
   • Distances to the right of the origin (along +x-axis) are positive.
   • Distances to the left of the origin (along –x-axis) are negative.
   • Distances above the principal axis (along +y-axis) are positive.
   • Distances below the principal axis (along –y-axis) are negative.

Mirror Formula and Magnification

Mirror Formula

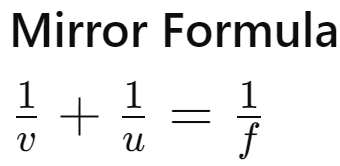
• u: Object distance
• v: Image distance
• f: Focal length

Magnification

​

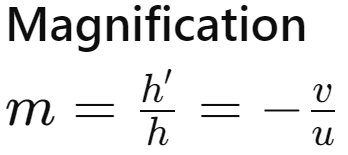
• h: Height of the object
• h’: Height of the image
• A positive magnification indicates a virtual image, while a negative magnification indicates a real image.

• Signs in Magnification:
  • Positive 𝑚: Virtual image (erect).
  • Negative 𝑚: Real image (inverted).

Example Problems

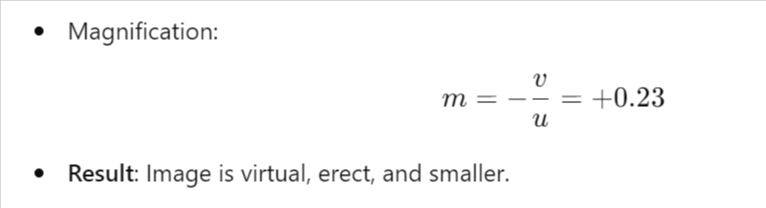
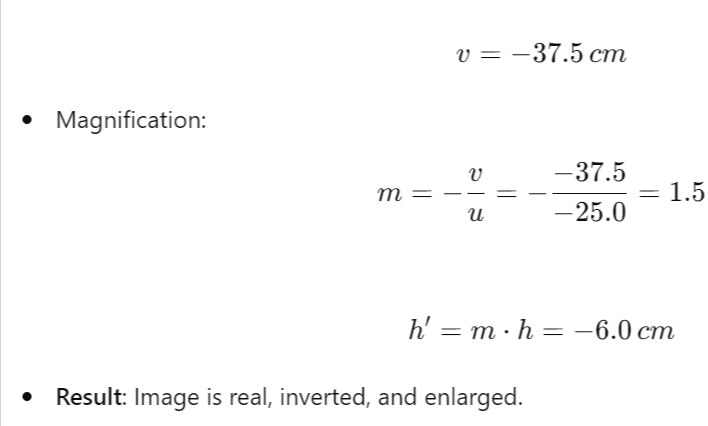
Summary

• The sign convention helps in solving problems related to spherical mirrors.
• The mirror formula and magnification are essential for understanding image formation.

Refraction of Light

What is Refraction?

• Light travels in straight lines in a single medium.
• When light enters from one transparent medium to another, it changes direction.
• Examples:
  • Bottom of a water tank looks raised.
  • Letters appear raised through a thick glass slab.
  • A pencil in water looks bent.
  • A lemon in water looks bigger.
  • Twinkling of stars, formation of rainbow, etc.

Why Does Refraction Happen?

• Light from the part of the pencil inside water seems to come from a different direction than the part above water.
• This makes the pencil look displaced at the water surface.
• The effect differs with different media like water, kerosene, or glass.

Activities to Understand Refraction

Refraction through a Rectangular Glass Slab

Why Does Refraction Occur?

• Due to a change in the speed of light between different media.
• Refraction follows certain laws.

Laws of Refraction

1. First Law:
   • The incident ray, refracted ray, and normal all lie in the same plane.
2. Snell’s Law:
   • Ratio of sine of the angle of incidence to the sine of the angle of refraction is constant (refractive index).

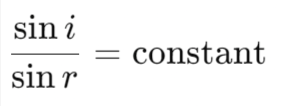
• This constant is the refractive index of the second medium relative to the first.

The Refractive Index

What is Refractive Index?

• Light changes direction when it moves from one transparent medium to another.
• This change in direction is measured by the refractive index.
• Refractive index relates to the speed of light in different media.

Speed of Light

• Fastest in vacuum: 3×10⁸ m/s.
• Slightly slower in air.
• Much slower in glass and water.

Calculating Refractive Index

• When light travels from medium 1 to medium 2:

• Refractive index of medium 1 with respect to medium 2:

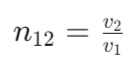
Absolute Refractive Index

• If medium 1 is vacuum or air:

Examples from Table 9.3

• Water: 𝑛𝑤=1.33
• Crown glass: 𝑛𝑔=1.52

Optical Density

• Refractive index indicates how optically dense a medium is.
• Higher refractive index = optically denser.
• Lower refractive index = optically rarer.
• Speed of light is higher in a rarer medium and lower in a denser medium.

Refraction by Spherical Lenses

What is a Lens?

• Transparent material with at least one spherical surface.
• Types of lenses:
  • Convex lens (thicker in the middle, converges light rays).
  • Concave lens (thicker at the edges, diverges light rays).

Terms Related to Lenses

• Centres of Curvature (C1, C2): Centers of the spheres forming the lens surfaces.
• Principal Axis: Imaginary line through the centers of curvature.
• Optical Centre (O): Central point of the lens.
• Aperture: Effective diameter of the lens.

Principal Focus

• Convex Lens: Parallel rays converge at the principal focus.
• Concave Lens: Parallel rays appear to diverge from the principal focus.
• Principal Focus (F): Point where rays converge or appear to diverge.
• Focal Length (f): Distance from the optical centre to the principal focus.

Image Formation by Lenses

How Lenses Form Images

Lenses form images by refracting light. Let’s see how this works for convex and concave lenses.

Convex Lens

Concave Lens

Conclusion:

• A concave lens always forms a virtual, erect, and diminished image, regardless of the object’s position.

Image Formation Using Ray Diagrams

Ray Diagrams

1. Convex Lens:
   • Parallel Ray: Passes through the principal focus on the other side after refraction.
   • Focus Ray: Emerges parallel to the principal axis after passing through the focus.
   • Central Ray: Passes through the optical center without deviation.
2. Concave Lens:
   • Parallel Ray: Appears to diverge from the principal focus after refraction.
   • Focus Ray: Emerges parallel to the principal axis.
   • Central Ray: Passes through the optical center without deviation.

Example Ray Diagrams

• Convex Lens: Images formed for various object positions.
• Concave Lens: Images formed for different object positions.

Sign Convention for Spherical Lenses

Sign Convention Rules

• Similar to spherical mirrors, but all measurements are from the optical center.
• Convex Lens: Focal length is positive.
• Concave Lens: Focal length is negative.
• Apply appropriate signs for object distance (u), image distance (v), focal length (f), object height (h), and image height (h’).

Lens Formula and Magnification

Lens Formula

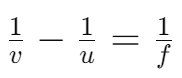
• This formula is general and valid for any spherical lens.
• Be careful with signs when solving problems.

Magnification

• Magnification is the ratio of the height of the image (h’) to the height of the object (h).

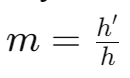
• Magnification is also related to object distance (u) and image distance (v):

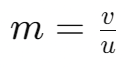
Example 9.3: Concave Lens

• Focal Length: −15 cm
• Image Distance: −10 cm
• Object Distance: Find using lens formula

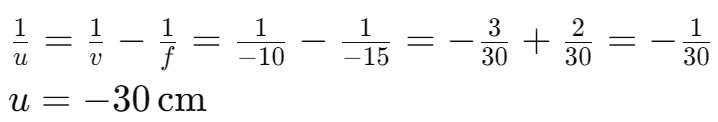
• Magnification:

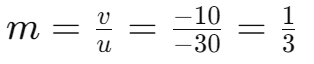
• The image is erect and virtual, one-third the size of the object.

Example 9.4: Convex Lens

• Object Height: 2 cm
• Focal Length: 10 cm
• Object Distance: −15 cm

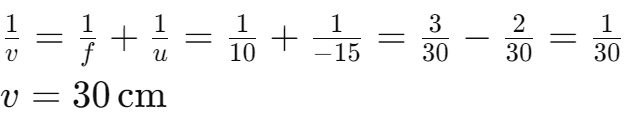
• Height of Image:

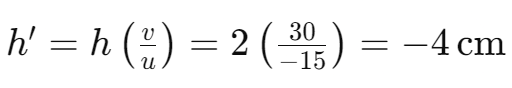
• The image is real, inverted, and twice the size of the object.

Power of a Lens

What is Power?

• Power measures the lens’s ability to converge or diverge light.
• Defined as the reciprocal of the focal length:

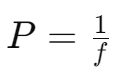
• SI Unit: Dioptre (D)
  • If 𝑓 is in meters, then power is in dioptres.
  • 1 D=1 m−1

Power of Different Lenses

• Convex Lens: Positive power.
• Concave Lens: Negative power.

Using Powers in Optical Instruments

• Combining lenses: The net power 𝑃P is the sum of individual powers:
• 𝑃=𝑃1+𝑃2+𝑃3+…
• Opticians use this to prescribe lenses by adding the powers of different corrective lenses.

Example

• Combining lenses of power +2.0 D and +0.25 D results in a lens of power +2.25 D
• This method helps design lenses for cameras, microscopes, and telescopes to minimize defects and improve image quality.

Chapter Summary:

• Light seems to travel in straight lines.
• Mirrors and lenses form images of objects. Images can be either real or virtual, depending on the position of the object.
• Reflecting surfaces obey the laws of reflection. Refracting surfaces obey the laws of refraction.
• New Cartesian Sign Conventions are followed for spherical mirrors and lenses.
• Mirror formula ​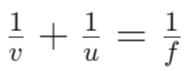 gives the relationship between object-distance (u), image-distance (v), and focal length (f) of a spherical mirror.
• The focal length of a spherical mirror is equal to half its radius of curvature.
• Magnification produced by a spherical mirror is the ratio of the height of the image to the height of the object.
• A light ray traveling obliquely from a denser medium to a rarer medium bends away from the normal. A light ray bends towards the normal when it travels obliquely from a rarer to a denser medium.
• Light travels in vacuum with an enormous speed of 3×10⁸ m/sThe speed of light is different in different media.
• The refractive index of a transparent medium is the ratio of the speed of light in vacuum to that in the medium.
• In a rectangular glass slab, refraction takes place at both air-glass and glass-air interfaces. The emergent ray is parallel to the direction of the incident ray.
• Lens formula ​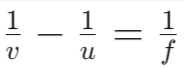 gives the relationship between object-distance (u), image-distance (v), and focal length (f) of a spherical lens.
• Power of a lens is the reciprocal of its focal length. The SI unit of power of a lens is dioptre.