Motion

Understanding Motion

• Everyday Motion: We see objects either at rest or in motion. Examples:
  • Birds flying
  • Fish swimming
  • Blood flowing
  • Cars moving
• Universal Motion: Everything from atoms to galaxies is in motion.

Perceiving Motion:

• Direct Perception: We see an object moving when its position changes over time.
• Indirect Evidence: Sometimes we infer motion by observing other things, like dust moving to know air is in motion.

Earth’s Motion:

• Phenomena: Sunrise, sunset, and changing seasons are due to Earth’s motion.
• Observation: We don’t perceive Earth’s motion directly because we are moving with it.

Relative Motion:

• Example: In a moving bus:
  • Passengers see roadside trees moving backward.
  • A person on the roadside sees the bus and passengers moving.
  • Inside the bus, passengers see each other as stationary.
• Conclusion: Motion can appear different from different perspectives.

• Complex Motion: Objects can move in straight lines, circles, rotate, or vibrate.

Types of Motion:

1. Motion Along a Straight Line: Simplest form of motion.
2. Circular Motion: Movement along a circular path.
3. Rotational Motion: When an object spins around an axis.
4. Vibrational Motion: When an object moves back and forth rapidly.

Activities and Discussions

Think and Act:

• Dangerous Motion: Erratic motions like floods or hurricanes can be dangerous.
• Controlled Motion: Useful in things like hydro-electric power generation.
• Importance of Study: Understanding and controlling erratic motion is important for safety and technology.

Describing Motion

Reference Point:

• Example: A school 2 km north of a railway station.
• Reference Point: The railway station is the reference point.
• Origin: The reference point from which positions are measured.

Motion Along a Straight Line

• Simplest Motion: Motion along a straight path.
• Example: Object moving from point O to A, then back to B and C.

Distance and Displacement:

• Distance:
  • Total path length covered.
  • Example: OA + AC = 60 km + 35 km = 95 km.
  • Only the numerical value (magnitude) matters.
• Displacement:
  • Shortest distance from initial to final position.
  • Example: From O to C through A, the displacement is the direct distance from O to C.

Example Breakdown:

1. O to A:
   • Distance: 60 km
   • Displacement: 60 km
2. O to A to B:
   • Distance: 60 km + 25 km = 85 km
   • Displacement: 35 km
3. O to A and back to O:
   • Distance: 60 km + 60 km = 120 km
   • Displacement: 0 km (initial and final positions are the same)

Key Points:

• Distance is the total path traveled.
• Displacement is the shortest path from start to end.
• Displacement can be zero if the object returns to the start point, but the distance will still be the total path covered.

Activities

Uniform and Non-Uniform Motion

Uniform Motion:

• Definition: When an object covers equal distances in equal intervals of time.
• Example:
  • An object travels 5 meters every second consistently.

Non-Uniform Motion:

• Definition: When an object covers unequal distances in equal intervals of time.
• Examples:
  • A car moving on a crowded street.
  • A person jogging in a park.

Measuring the Rate of Motion

Understanding Speed:

• Definition: Speed is the distance traveled by an object in a unit time.
• Units:
  • Metres per second (m/s)
  • Centimetres per second (cm/s)
  • Kilometres per hour (km/h)
• Formula: Speed (v) = Distance (s) / Time (t)

Average Speed:

• Definition: Used for non-uniform motion where speed varies.
• Formula: Average Speed = Total Distance / Total Time
• Example:
  • A car travels 100 km in 2 hours.
  • Average speed = 100 km / 2 h = 50 km/h.

Example Problem:

• Scenario: An object travels 16 meters in 4 seconds, then another 16 meters in 2 seconds.
• Solution:
  • Total distance = 16 m + 16 m = 32 m.
  • Total time = 4 s + 2 s = 6 s.
  • Average speed = 32 m / 6 s = 5.33 m/s.

Key Points to Remember:

• Uniform motion: Equal distances in equal times.
• Non-uniform motion: Unequal distances in equal times.
• Speed: Distance per unit time.
• Average speed: Total distance divided by total time.

Measuring the Rate of Motion

Understanding Speed:

• Definition: Speed is how fast an object moves, measured as distance traveled per unit time.
• SI Unit: The standard unit of speed is meters per second (m/s). Other units include kilometers per hour (km/h) and centimeters per second (cm/s).

Average Speed:

• Formula: Average speed = Total distance traveled / Total time taken
• Example: A car travels 100 km in 2 hours. Average speed = 100 km / 2 h = 50 km/h.

Example Calculation:

• Scenario: An object travels 16 m in 4 s, then 16 m in 2 s.
• Solution:
  • Total distance = 16 m + 16 m = 32 m
  • Total time = 4 s + 2 s = 6 s
  • Average speed = 32 m / 6 s = 5.33 m/s

Speed with Direction (Velocity)

• Definition: Velocity is speed in a specific direction.
• Uniform Velocity: Constant speed in a straight line.
• Variable Velocity: Changes in speed or direction.
• Average Velocity Formula: (Initial velocity + Final velocity) / 2

Example Calculations:

• Average Speed Example:
  • Scenario: Car’s odometer reads 2000 km at start, 2400 km at end of trip taking 8 hours.
  • Solution:
    • Distance = 2400 km – 2000 km = 400 km
    • Average speed = 400 km / 8 h = 50 km/h
    • Convert to m/s: 50 km/h = 13.9 m/s
• Usha’s Swimming Example:
  • Scenario: Usha swims 180 m in a 90 m pool in 1 minute.
  • Solution:
    • Total distance = 180 m
    • Displacement = 0 m (back to starting point)
    • Average speed = 180 m / 60 s = 3 m/s
    • Average velocity = 0 m / 60 s = 0 m/s

Activities:

Key Takeaways

• Speed measures how fast something moves.
• Average speed helps understand overall motion, even if speed varies.
• Velocity includes direction, making it more comprehensive than speed.
• Understanding these concepts helps describe and analyze different types of motion.

Rate of Change of Velocity

Uniform Motion:

• Velocity stays constant.
• Change in velocity = 0.

Non-Uniform Motion:

• Velocity changes over time.
• Different values at different times and points.

Acceleration:

• Measures change in velocity per unit time.
• Formula:

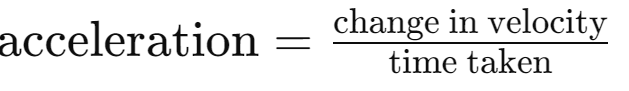
• If velocity changes from 𝑢 to v in time 𝑡​

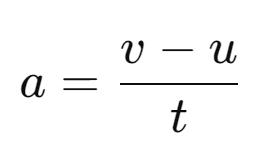
• Positive acceleration: Direction of velocity.
• Negative acceleration: Opposite to the direction of velocity.
• SI unit: m/s²

Uniform Acceleration:

• Velocity increases/decreases equally in equal time intervals.
• Example: Freely falling body.

Non-Uniform Acceleration:

• Velocity changes by unequal amounts in equal time intervals.
• Example: A car increasing speed unequally.

Activity 7.8: Examples of Acceleration

• Acceleration in direction of motion: A car speeding up.
• Acceleration against motion: A car slowing down.
• Uniform acceleration: A ball rolling down a slope at a constant rate.
• Non-uniform acceleration: A car speeding up unevenly.

Example 7.4: Calculating Acceleration

First Case:

• Starts from rest: 𝑢=0
• Final velocity: 𝑣=6 m/s.
• Time: 𝑡=30s.
• Acceleration:

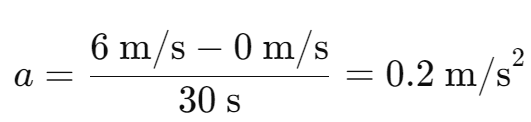
Second Case:

• Initial velocity: 𝑢=6 m/s.
• Final velocity: 𝑣=4 m/s.
• Time: 𝑡=5 s.
• Acceleration:

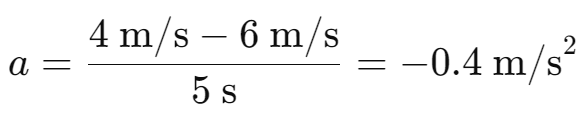
• First case acceleration: 0.2 m/s².
• Second case acceleration: −0.4 m/s².

Graphical Representation of Motion

Introduction to Graphs:

• Graphs are useful to present information clearly.
• Example: Bar graphs in cricket show run rate per over.
• Line graphs help solve equations with two variables.

Describing Motion with Line Graphs:

• Line graphs can show how distance or velocity depends on time.

Distance–Time Graphs

Basics:

• Show an object’s position change over time.
• Time is on the x-axis, distance on the y-axis.
• Useful for various motion conditions: uniform speed, non-uniform speed, rest.

Uniform Speed:

• Object travels equal distances in equal time intervals.
• Distance is directly proportional to time.
• Graph of distance vs. time is a straight line.
• Example: Segment OB in the graph shows uniform distance increase.

Calculating Speed:

• Pick a small part of the distance-time graph.
• Draw horizontal and vertical lines from points A and B to meet at C, forming triangle ABC.
• AC represents time interval (𝑡2−𝑡1), and BC represents distance (𝑠2−𝑠1).
• Speed, 𝑣, is calculated as:

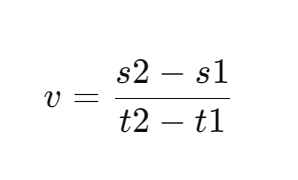
Accelerated Motion:

• Different shape from uniform motion graph.
• Example: A car’s distance-time graph shows non-linear variation, indicating non-uniform speed.

Key Points:

• Uniform Motion: Straight line on graph.
• Non-Uniform Motion: Curved line on graph.
• Graph Use: Determine speed from slope of the line.

Velocity-Time Graphs

Introduction:

• Shows how velocity changes over time.
• Time on x-axis, velocity on y-axis.

Uniform Velocity:

• Velocity-time graph is a straight line parallel to x-axis.
• Example: Car moving at 40 km/h.

Calculating Displacement:

• Displacement = velocity × time.
• Area under velocity-time graph equals displacement.
• Example: Distance moved by car between time 𝑡1 and t2:

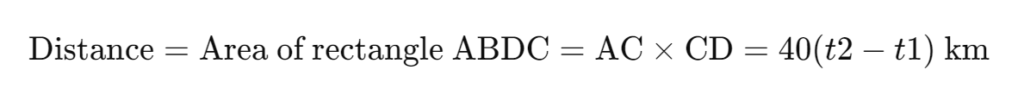
Uniformly Accelerated Motion:

• Velocity-time graph is a straight line.
• Velocity changes equally in equal time intervals.
• Example: Car’s velocity recorded every 5 seconds.

Calculating Distance in Accelerated Motion:

• Area under velocity-time graph gives distance.
• Example: Distance travelled by car (Figure 7.6):Distance=Area under graph ABCDE=Area of rectangle ABCD+Area of triangle ADEDistance=Area under graph ABCDE=Area of rectangle ABCD+Area of triangle ADE=𝐴𝐵×𝐵𝐶+12(𝐴𝐷×𝐷𝐸)=AB×BC+21​(AD×DE)

Non-Uniformly Accelerated Motion:

• Velocity-time graph can have any shape.
• Example:
  • Decreasing velocity over time (Figure 7.7a).
  • Non-uniform variation in velocity (Figure 7.7b).

Activities

Key Points:

• Uniform Velocity: Straight line parallel to x-axis.
• Uniform Acceleration: Straight line with a slope.
• Non-Uniform Acceleration: Curved or irregular lines.
• Displacement: Area under the velocity-time graph.

Equations of Motion

• When an object moves with uniform acceleration along a straight line, its velocity, acceleration, and distance covered can be related by equations of motion.

Equations of Motion:

• Velocity-Time Relation:

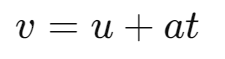
• Position-Time Relation:

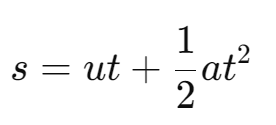
• Position-Velocity Relation:

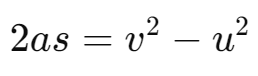
Variables:

• 𝑢: Initial velocity
• 𝑣: Final velocity
• 𝑎: Acceleration
• 𝑡: Time
• 𝑠: Distance traveled

Example 7.5: Train Accelerating

• Problem:
  • Starts from rest, reaches 72 km/h in 5 minutes.
  • Find acceleration and distance traveled.
• Solution:

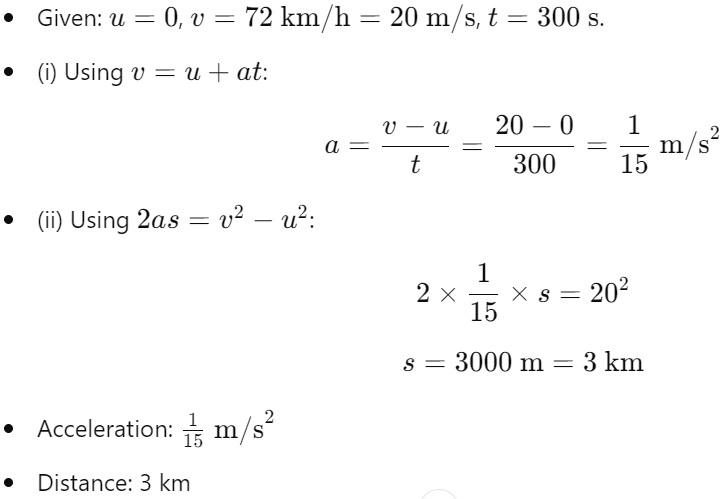
Example 7.6: Car Accelerating

• Problem:
  • Accelerates from 18 km/h to 36 km/h in 5 seconds.
  • Find acceleration and distance covered.
• Solution:

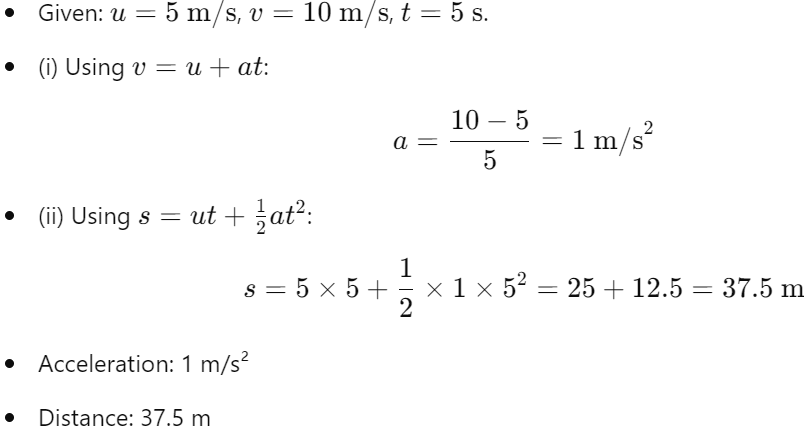
Example 7.7: Car Decelerating

• Problem:
  • Brakes produce acceleration of -6 m/s². Car stops in 2 seconds.
  • Find distance traveled.
• Solution:

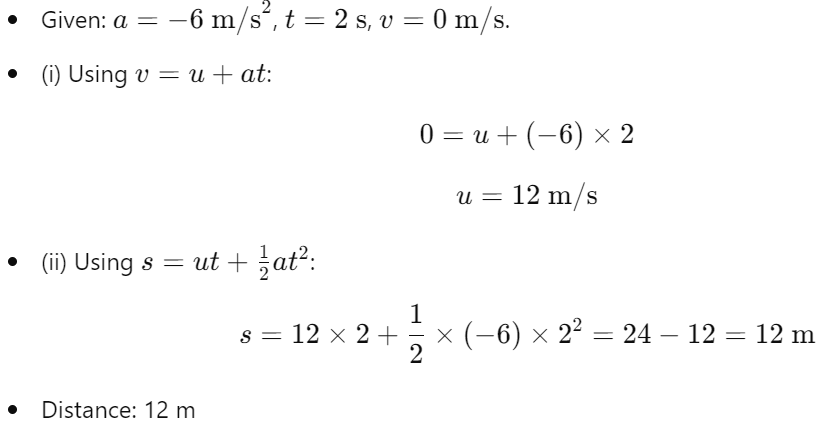
Key Points:

• Equations of motion help relate velocity, acceleration, and distance.
• Uniform acceleration makes calculations straightforward using these equations.
• Practical examples show how to apply these equations to real-life situations.

Uniform Circular Motion

• An object accelerates when its velocity changes.
• This change can be in magnitude (speed) or direction.

Changing Direction without Changing Speed:

• Example: An athlete running on different shaped tracks (rectangle, hexagon, octagon).
• As the number of sides increases, the track approximates a circle.
• Running on a circular track at constant speed means the athlete changes direction continuously but not speed.

Uniform Circular Motion:

• When an object moves in a circular path with constant speed.
• Even though speed is constant, the object accelerates because the direction changes.

Calculating Speed on a Circular Path:

• Circumference of circle: 2𝜋𝑟(where 𝑟 is the radius).
• Speed 𝑣=2𝜋𝑟/𝑡 where t is the time for one round).

Examples of Uniform Circular Motion:

• Hammer or discus throw in sports.
• Motion of the moon around the earth.
• Satellite orbiting the earth.
• Cyclist on a circular track at constant speed.

Key Points:

• Uniform circular motion involves constant speed but continuous change in direction.
• This type of motion is common in both daily life and celestial movements.

Chapter Summary:

• Motion is a change of position.
• Motion can be described by distance moved or displacement.
• Motion can be uniform (constant velocity) or non-uniform (changing velocity).
• Speed is the distance covered per unit time.
• Velocity is the displacement per unit time.
• Acceleration is the change in velocity per unit time.
• Uniform and non-uniform motions can be shown through graphs.
• Motion with uniform acceleration can be described by these equations:

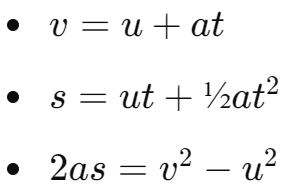
• In these equations:
  • 𝑢 is the initial velocity.
  • 𝑎 is uniform acceleration.
  • 𝑡 is time.
  • 𝑣 is final velocity.
  • 𝑠 is the distance traveled in time 𝑡t.
• Uniform circular motion is when an object moves in a circular path with uniform speed.